Author
Nate Wichmann
Mentors
April South, Biological Sciences and Andy Schumpert, Biological Sciences
Abstract
Many animals live in social groups for a variety of reasons, whether it is for hunting strategies, predator avoidance, or enhanced resource acquisition. These groups often develop a social network and/or dominance hierarchy within the population, with certain individuals gaining advantages or disadvantages based upon one’s rank within a group. Dominance hierarchies can be assessed on the grounds of structure, and, more recently, steepness. Structure can be assessed by determining and comparing the rank of each individual (quantified by David’s scores). These scores can then be plotted and analyzed to determine the steepness of the dominance hierarchy. A dominance hierarchy with a high degree of steepness has a greater separation between adjacent ranks than a hierarchy with a low degree of steepness.
This study examines a group of eight Western Lowland Gorillas (Gorilla gorilla gorilla) at the Cincinnati Zoo and Botanical Garden (CZBG) by observing resolved agonistic behaviors in order to quantify dominance and rank individuals using David’s scores, which are then used to quantify the steepness of the dominance hierarchy.
The group in this study exhibits a structure that resembles a pyramidal organization, with a small group of individuals exhibiting a significantly greater David’s score than a larger group of lower ranked individuals. The steepness was calculated to be 0.307, which is a fairly shallow slope. This may be a result of the captive setting, where the competition for resources and external pressures are limited.
Introduction
Hierarchical populations are often examined and described in terms of the dominant individual/group of individuals or their dominance patterns. Through observation of resolved agonistic behaviors, individuals can be sorted into discreet ranks within a population. Agonistic behaviors can include vocalization, physical aggression, or postural/locomotive displays directed at another individual with or without physical contact (Watts, 1994) and are often utilized in contest for resources such as food, water, or space. For an interaction to be considered resolved, one individual must emerge as a clear victor, demonstrated by retreat, defensive, or submissive action by the receiving individual. Unresolved agonistic interactions show no clear winner or loser in the interaction, demonstrated by the receiving individual ignoring the agonistic behavior of the initiator or returning aggression from the initiator (Watts, 1994).
A common method of quantifying dominance is ranking each individual based upon it’s David’s Score (DS), a value determined by the proportion of “wins” and “losses” during agonistic interactions between individuals in every possible dyad (interacting pair) within a group (David, 1987). Based on these interactions, dominance hierarchies can assume a number of forms: linear (A>B>C>D>…), non-linear (A>B, B>C, C>A), pyramidal (A>[B+C+D], or classed ([A+B]>[C+D+E+F]) (Preuschoft & van Schaik, 2000). Beyond simply ranking individuals on their respective dominance, the dominance steepness within a population has recently been gaining more attention. Dominance steepness is a measure of the difference in dominance between ranks within a population (i.e. the degree of separation between adjacently ranked individuals) (de Vries et al., 2006). For example, in a group of two individuals, Individual A may be dominant over Individual B, thus occupying ranks 1 and 2, respectively. By examining the steepness within their relationship, one can determine how dominant Individual A is over Individual B. A steeper relationship indicates a greater degree of dominance of Individual A over Individual B. This method can also be applied to a larger group consisting of pairs to determine the relative increase in dominance between ranks within the group. In this study, a group of eight captive gorillas was observed and sorted into a dominance hierarchy based on David’s score through analysis of success or failure in dyadic agonistic interactions. de Vries’ method and associated statistical test (de Vries et al., 2006) were utilized to quantify the steepness of the constructed hierarchy.
Western lowland gorillas (Gorilla gorilla gorilla) typically live in stable groups with an average size of approximately eight individuals consisting of a single fully mature male, and a variable number of adult females, sub-adult males, and juveniles/infants (Parnell, 2002). These groups exhibit a range of behaviors that establish a social network and a dominance hierarchy within the group. The individuals observed in this study were housed at the Cincinnati Zoo & Botanical Garden (CZBG) in a group consisting of a single, adult silverback male, four adult females and three infant/juvenile females, which generally reflects that of a “juvenile” group composition as described by Parnell (2002). Although this captive population does reflect a natural composition, it has been artificially constructed through various means (additions and subtractions from the group, adoptive children, etc.). Furthermore, the husbandry staff provide daily, preferential feeding of the perceived dominant male and female while on exhibit, which reinforces a specific dominance structure.
These factors present potential for deviation from the dominance hierarchy characteristics of a wild population, though the group still provides an adequate model for studying dominance interactions and hierarchical steepness. In accounting for the captive state of the group and the hierarchy supported by the husbandry staff, I anticipate a linear dominance structure in which Jomo possesses the highest rank and Asha possesses the highest rank among female members. I also predict a high level of dominance steepness within the group and the ranking of adolescents will reflect the rankings of their respective mothers.
Materials and Methods
This study focused on a group of captive gorillas at the CZBG consisting of eight individuals. The group consisted of one silverback male and seven females ranging from ages 1-47 (gorillas typically living 30-40 years in the wild). Three mother/offspring pairings exist within the group (Asha/Mondika, Anju/Elle, and M’Linzi/Gladys). Two of the offspring, Mondika and Elle, were sired by the resident silverback male, Jomo, while Gladys was born at the Gladys Porter Zoo and introduced to the CZBG group with M’Linzi serving as an adoptive mother. Individual characteristics and familial relations are listed in Figures 1 and 2:
CZBG Gorilla Study Population Profile
|
Name |
Sex |
Age |
|
Jomo |
Male |
25 |
|
Samantha |
Female |
47 |
|
Asha |
Female |
14 |
|
Anju |
Female |
16 |
|
M’Linzi |
Female |
34 |
|
Gladys |
Female |
4 |
|
Mondika |
Female |
2 |
|
Elle |
Female |
1 |
Figure 1: Individuals and their respective sexes and ages in the study group at the Cincinnati Zoo and Botanical Garden.
Phylogenetic Tree for Gorillas at CZBG
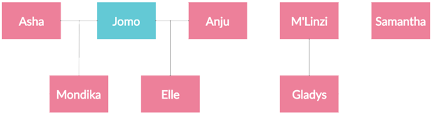
Figure 2: Familial relations among group members. Horizontal lines indicate matings; vertical lines indicate offspring. Note: M’Linzi did not birth Gladys but does serve as an adoptive mother.
Data collection occurred through in person observation of individual behaviors in August of 2017 for approximately fifteen total hours of observation. Observations typically occurred in one to three hour increments between the hours of 10:00am and 2:00pm.
In order to determine the rank of individuals within the dominance hierarchy, resolved agonistic interactions and their respective winners and losers were recorded for each and every dyad within the population. These wins and losses were then used to calculate David’s Scores (DS) (David, 1987) for each individual, with a greater score indicating a higher rank of dominance within the group. DS are based on the proportion of wins by individual i over individual j in all of their interactions (Pij). The proportion of wins by j over i (Pji) is equal to 1-Pij. However, de Vries’ method (de Vries et al., 2006) of DS calculation was used in this study as it compensates for asymmetry in the number of interactions between dyads by utilizing a chance corrected Dyadic Dominance Index (Dij) in in place of Pij when calculating DS. As such, Pji can also be replaced by 1-Dij. Dij can be calculated as follows:
In this equation sij is equal to the number of wins by i over j, and nij is the total number of interactions between i and j. Using the calculated Dij values, DS for individual i can then be determined using the following equation:
In this equation, w is equal to the sum of an individual’s dyadic dominance indexes {}, and w2 is the sum of individual i’s dyadic dominance indexes weighted by individual j’s w value {}, where N is the number of individuals in the group. is equal to the sum of an individual’s values, and is representative of the sum of an individual’s Dji values weighted by the values of individual j { and , respectively} (de Vries et al., 2006).
It is then necessary to convert all DS to normalized David’s scores (NormDS), allowing individuals to be more easily ranked and classified within their group. This conversion also allows for the appropriate plotting of points in order to determine the steepness of the dominance hierarchy. NormDS will be a value between 0 and N where N is the number of individuals in a group (N=8 in the CZBG Study Group). NormDS can be calculated using the following equation:
In this equation, DS is an individual’s David’s score, N is equal to the number of individuals in a group, and MaxDS is equal to the maximum David’s score achievable by an individual in a group of size N, which can be calculated via .
Results were then organized on a scatter plot in descending order of dominance rank (based on NormDS) on the X-axis, and NormDS on the Y axis. The line of best fit was then determined, and the absolute value of the slope of this line was accepted as the steepness of the dominance hierarchy. To test for significance, this process was repeated 2,000 times using random whole numbers between 0 and N for Dij for each dyad in order to construct a random frequency distribution which was then compared to the observed results to test if the results differed from random.
Results
There were a total of 55 agonistic interactions within the group during the study period, 51 of which were resolved. The outcomes of resolved dyadic agonistic interactions are recorded in Figure 3. Figure 4 contains the dyadic dominance indexes (Dij), David’s scores (DS), normalized David’s scores (NormDS), as well as the w, w2, l, and l2 values that were used in order to determine DS and NormDS for each individual. The lone silverback male possessed the highest ranking within the group (NormDS: 5.07), followed by a single female, Asha, with a NormDS of 4.11, which is significantly higher than any other female in the group. The next five individuals (adults and juveniles) are relatively even in dominance with NormDS values ranging only from 3.48 to 3.02. This leaves only Gladys, a juvenile, with a NormDS value of 2.25 as the least dominant individual in the group (Figure 4)
Dyadic Wins and Losses
|
Asha |
Anju |
M'Linzi |
Samantha |
Jomo |
Elle |
Mona |
Gladys |
|
|
Asha |
X |
5 |
5 |
1 |
0 |
1 |
0 |
5 |
|
Anju |
2 |
X |
0 |
1 |
0 |
0 |
0 |
1 |
|
M'Linzi |
0 |
0 |
X |
1 |
0 |
0 |
0 |
1 |
|
Samantha |
0 |
0 |
0 |
X |
0 |
0 |
0 |
1 |
|
Jomo |
6 |
3 |
2 |
1 |
X |
2 |
4 |
2 |
|
Elle |
0 |
0 |
0 |
0 |
0 |
X |
0 |
0 |
|
Mona |
0 |
0 |
0 |
0 |
0 |
0 |
X |
6 |
|
Gladys |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
X |
Figure 3: Dyadic wins and losses in agonstic interactions among each dyad in the group of study. Read left to right, the table indicates dyadic victories. Read top to bottom, the table indicates dyadic losses. Thus, Anju had two wins over Asha, and Asha had five wins over Anju (rows). Asha had six losses to Jomo (Asha’s column).
Statistical Calculations for Dyadic Interactions
|
Asha |
Anju |
M'Linzi |
Sam |
Jomo |
Elle |
Mona |
Gladys |
L |
L2 |
DS |
NormDS |
|
|
Asha |
X |
0.688 |
0.917 |
0.750 |
0.071 |
0.750 |
0.000 |
0.917 |
1.908 |
3.413 |
4.846 |
4.106 |
|
Anju |
0.313 |
X |
0.000 |
0.750 |
0.125 |
0.000 |
0.000 |
0.750 |
2.063 |
4.243 |
-0.142 |
3.482 |
|
M'Linzi |
0.083 |
0.000 |
X |
0.750 |
0.167 |
0.000 |
0.000 |
0.750 |
2.250 |
4.636 |
-1.600 |
3.300 |
|
Sam |
0.250 |
0.250 |
0.250 |
X |
0.250 |
0.000 |
0.000 |
0.750 |
3.250 |
6.653 |
-3.829 |
3.021 |
|
Jomo |
0.929 |
0.875 |
0.833 |
0.750 |
X |
0.833 |
0.900 |
0.833 |
1.046 |
2.756 |
12.575 |
5.072 |
|
Elle |
0.250 |
0.000 |
0.000 |
0.000 |
0.167 |
X |
0.000 |
0.000 |
1.583 |
2.303 |
-1.454 |
3.318 |
|
Mona |
0.000 |
0.000 |
0.000 |
0.000 |
0.100 |
0.000 |
X |
0.813 |
1.088 |
1.844 |
-0.459 |
3.443 |
|
Gladys |
0.083 |
0.250 |
0.250 |
0.250 |
0.167 |
0.000 |
0.188 |
X |
4.813 |
9.176 |
-9.938 |
2.258 |
|
w |
4.092 |
1.938 |
1.750 |
1.750 |
5.954 |
0.417 |
0.913 |
1.188 |
X |
X |
X |
X |
|
w2 |
6.075 |
4.226 |
3.536 |
4.324 |
10.424 |
2.015 |
1.560 |
2.864 |
X |
X |
X |
X |
Figure 4: Table of dyadic dominance indices (Dij) and all values (w, w2, l, l2) used to calculate David’s score (DS) and normalized David’s score (Norm DS).
The trend of dominance within the group is not entirely linear, with the male (Jomo) being far more dominant than the rest of the group, and one female (Asha) being significantly more dominant than all other females. The rest of the females, with the exception of Gladys, had very similar dominance scores. As such, this hierarchy resembles a pyramidal or classed structure, with a group of individuals extremely close in rank being dominated by a smaller number of dominant individuals (Figure 5). Despite the high level of dominance exhibited by the most dominant individuals, the relative similarity of NormDS in the middle ranks yields a shallow dominance steepness of 0.307 (Figure 5). This result is significant with no results out of 2,000 randomized simulations of the study exceeding the observed value of steepness (p-value: 0.005).
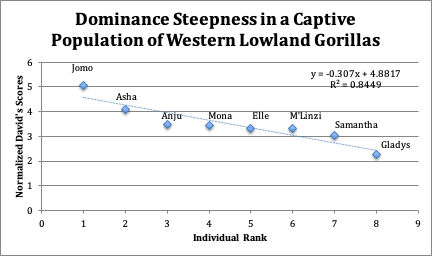 Figure 5: Graph depicting individual Normalized David’s Scores in decreasing order
used to determine steepness of the dominance hierarchy. The equation represents the
line of best fit, with a slope of -0.307. R2 is a measure representing how well the line fits the data. R2 can range from 0-1 with values closer to 1 indicating a stronger relationship between
the slope of the line and the slope of the data.
Figure 5: Graph depicting individual Normalized David’s Scores in decreasing order
used to determine steepness of the dominance hierarchy. The equation represents the
line of best fit, with a slope of -0.307. R2 is a measure representing how well the line fits the data. R2 can range from 0-1 with values closer to 1 indicating a stronger relationship between
the slope of the line and the slope of the data.
Discussion
The ranking of individuals within the population is similar to what was predicted. Jomo, the dominant male, ranks at the top of the dominance ladder with a significantly greater NormDS than any other individual (Figure 2). He is followed by Asha, with a NormDS significantly greater than that of any other female (Figure 2); however, it is not known if Asha’s position would have occurred organically if this group were left to its own devices. Asha’s preferential feeding by the care staff, among other factors, likely contributes to her elevated position within the group, as this greater access to food resources mimics natural mechanisms of dominance in which higher ranking individuals assert their dominance to gain a greater portion of shared resources (Wright & Robbins, 2014). It can be determined though that Asha’s dominance is well engrained in the group. Clearly, she was victorious in interactions far more often than not, but the majority of her interactions were simple displacements rather than escalated violence. Rarity of escalated violence can indicate that individuals are well informed on the status of an opponent and the likely outcome and thus opt for low cost behaviors (Preuschoft & van Schaik, 2000).
It ought to be noted as well that the position of adult females is inversely related to age. Asha is the youngest and most dominant, while Samantha is the oldest and least dominant. However, while Samantha possesses only a single dyadic victory (over Gladys), she did engage in a number of unresolved agonistic interactions (i.e. mutual aggression), in which no clear winner was present, including interactions with Asha. This could potentially indicate that the relationship between Asha (the most dominant female) and Samantha is not fully established (de Vries et al., 2006) or that additional factors beyond the scope of this study are contributing to the structure of this dominance hierarchy. Furthermore, few resolved interactions existed between Samantha and any other adult members of the group. It has been observed that through repeated interactions with a given individual, agonistic interactions decrease in duration as a certain individual repeatedly establishes dominance (Barker et al., 1979). These factors may indicate that Samantha has a higher position within the group, as individuals may have avoided her due to a position of dominance established before the time period of the study.
One noticeable trend in the dominance hierarchy can be seen when comparing the subsets of adult females to infants/juveniles. The ranking of mothers in the group correlates to the ranking of their respective offspring, with Asha and M’Linzi being the most and least dominant, respectively, of the mothers and Mondika and Gladys in corresponding positions among the infants/juveniles. It can also be seen that the females with offspring, especially those that have mated with the dominant male, assume higher positions in the group. Samantha (NormDS: 3.02) is the only female without an associated juvenile and possesses the lowest rank among adult females, while M’Linzi, whose offspring was assumed via surrogacy assumes the next to lowest position in the hierarchy among adult females. These observations are supported by a similar study by Pusey (1997) displaying that dominant female chimpanzees within a linear hierarchy exhibit greater reproductive success, and their offspring often rise to higher levels of dominance than the offspring of less dominant individuals. One may also give further consideration to Gladys’ position as an adoptive juvenile independent of her mother due to the lack of true genetic/familial relations. As females mature into adulthood, they often will transfer from their natal group and join another group or solitary male; however, transfer is a task most commonly undertaken by sub-adult or young adult females (Parnell, 2002). Gladys has not yet reached those life stages, and would not transfer to another group at this age in a wild population. As such, the introduction of a foreign juvenile may play a part in relegating Gladys to the lowest rank among juveniles and infants.
The steepness of the curve is equal to 0.307, which passes the test for significance (p-value: <0.005). This indicates that the ranking of a given individual within this group experiences only a small change in dominance over or below an adjacent individual. In a study of a wild western lowland gorillas by Lodwick (2014), the majority of agonistic interactions were resolved and were associated with food monopolization, however, a greater degree of steepness was commonly present within a linear dominance hierarchy. In the CZBG population there is very little need for intra-group competition over food, as each member of the group receives an individualized diet of a specific size each day. Though competition for food is not prominent in this group, competition for access to the male may still be. According to Watts (1994), agonistic interactions occur more commonly in the context of access to reproductive resources than dietary resources when food cannot be easily monopolized (as demonstrated in the individualized diets of the CZBG group). The presence of competition for access to the male may potentially be visualized through correlation between the dominance of females and their offspring, as the more dominant individuals are those that possess offspring by the silverback, which is again supported by Pusey’s (1987) study on dominance and mating success in chimpanzees. It may be worthwhile to pursue further study in groups in which some females of reproductive age do not possess any offspring to further assess how the presence of offspring affects the context, frequency, and outcome of agonistic behaviors. Furthermore, assuming no major changes in group composition, the dominance of the infants and juveniles in the CBZG group ought to be observed in order to see how their current status translates into adulthood.
This information can be applied to the management of captive gorilla populations in reinforcing dominance hierarchies to minimize the occurrences of escalated violence between individuals, thus protecting them from harm. This data can also be used assist to in managing the introduction or removal of an individual to or from a group to assess the potential consequences of any artificial shifts in group composition.
About the Author
 Nate Wichmann
Nate Wichmann
My name is Nate Wichmann, and I am from Ryland Heights, Kentucky. I graduated from the University of South Carolina Honors College with a Bachelor’s of Science in Biology in 2018. I have since enrolled in the Auburn University College of Veterinary Medicine and am pursuing my Doctorate of Veterinary Medicine. This project was inspired by my interest in exotic animal medicine and conservation. I completed an internship at the Cincinnati Zoo and Botanical Garden in 2016 where I was responsible for the care of the institution’s primate collection, including the gorillas observed in this study. I completed similar research in support of Dr. April South’s research on the social network of miniature horses. The zoos and aquariums within the United States are an enormous reservoir of captive, non-solitary animals that are regularly relocated based on breeding recommendations in order to maintain genetic diversity for these ambassador animals. I saw this research as an opportunity to contribute to the operations of zoological institutions by helping to facilitate the introduction and integration of relocated animals to their new family groups. This project has shown me just what it takes to formulate and complete a research endeavor as well as the complexity of animal relationships that we often fail to see if we aren’t paying attention.
Special thanks are due to Dr. April South for inspiring my project as well as mentoring and supporting me throughout the entire process and Dr. Andy Schumpert reviewing and providing feedback on my study. I would also like to thank the Cincinnati Zoo and Botanical Garden, especially Ron Evans, Curator of the Primate Department, and the entire primate care staff for allowing me to observe and report on their gorilla population. This work was accepted to be presented at the 2018 International Gorilla Workshop.
Literature Cited
Barker, D. G., Murphy, J. B., & Smith, K. W. (1979). Social Behavior in a Captive Group of Indian Pythons, Python molurus (Serpentes, Boidae) with Formation of a Linear Social Hierarchy. Copeia,1979(3), 466. doi:10.2307/1443224
David, H. A. (1987). Ranking from Unbalanced Paired-Comparison Data. Biometrika,74(2), 432. doi:10.2307/2336160
Lodwick, J. L. (2014). Links between foraging strategies, feeding competition, and female agonistic relationships in wild western gorillas (Gorilla gorilla) [Unpublished doctoral dissertation]. Stony Brook University.
Parnell, R. J. (2002). Group size and structure in western lowland gorillas (Gorilla gorilla gorilla) at Mbeli Bai, Republic of Congo. American Journal of Primatology,56(4), 193-206. doi:10.1002/ajp.1074
Preuschoft S. & van Schaik CP. 2000. Dominance and communication: conflict management in various social settings. In: Aureli F, de Waal FBM, editors. Natural conflict resolution. Berkeley: University of California Press; 2000. pp. 77–105.
Pusey, A. (1997). The Influence of Dominance Rank on the Reproductive Success of Female Chimpanzees. Science,277(5327), 828-831. doi:10.1126/science.277.5327.828
de Vries, H., Stevens, J. M., & Vervaecke, H. (2006). Measuring and testing the steepness of dominance hierarchies. Animal Behaviour,71(3), 585-592. doi:10.1016/j.anbehav.2005.05.015
Watts, D. P. (1994). Agonistic relationships between female mountain gorillas (Gorilla gorilla beringei). Behavioral Ecology and Sociobiology, 34(5), 347–358. doi: 10.1007/s002650050050
Wright, E., & Robbins, M. M. (2014). Proximate mechanisms of contest competition among female Bwindi mountain gorillas (Gorilla beringei beringei). Behavioral Ecology and Sociobiology,68(11), 1785-1797. doi:10.1007/s00265-014-1788-6
